Research

My research is to use first-principles-based techniques such as density functional theory, effective Hamiltonian, and phenomenological method to study materials of fundamental and technological interests. I am interested in understanding and designing materials with intriguing properties and functionalities, e.g., ferroelectrics, multiferroics, and thermoelectrics. Another goal is to develop or improve computational methodologies to achieve state-of-the-art accuracy and efficiency.

Ferroelectrics and Multiferroics

Ferroelectrics (FE) are materials with spontaneous polarization that can be switched by an applied electric field. Multiferroics (MF) form an important class of materials that possess coupled long-range electric and magnetic orders. Such magneto-electric coupling is promising for designing new devices taking advantage of the control of magnetic properties by the application of an electric field; or vise versa. Polarization switching mechanisms and polarization-versus-electric field (P-E) hysteresis curves are fundamental and vitally affect its technological applications.

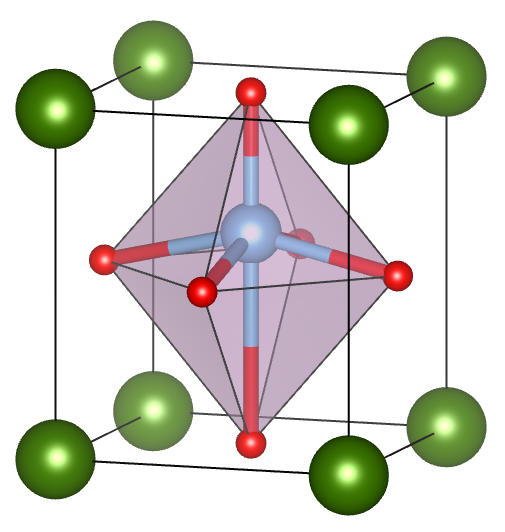
The intriguing interplay between the electric, magnetic degrees of freedom with structural, mechanic, and optical properties provide a very rich and interesting playground for a large variety of possiblities. Some interesting fundamental questions are: (i) What is the origin of ferroelectricity, antiferroelectricity (AFE), or specific magnetic structure? How does the phase transition occur? What are the temperature- or pressure-dependence of the order parameters? (ii) What is the switching mechanims? (iii) How to control magnetism with an electric field in multiferroics? (iv) What are the applications based on FE, AFE, or MF, and how to design novel material with improved performance?

The computational methods include density-functional-theory (DFT) calculations and effective Hamiltonian (Heff) technique, with the later being able to treat systems up to the order of millions of atoms. The Heff method can be used in Monte Carlo or Molecular Dynamics simulations to study the finite-temperaure or time-dependent dynamic properties, such as predicting equilibrium structures, phase transitions, hysteresis loop, polarization switching process, and response functions (dielectric permitivity, magnetic permeability), etc.

Thermoelectrics

Accurate prediction of transport properties from first-principles is desirable for thermoelectric applications. Combining the Boltzmann transport theory with the predictive power of density functional calculations, the electrical conductivity, Seebeck coefficient, electronic and lattice thermal conductivity can be computed within the diffusive transport regime.

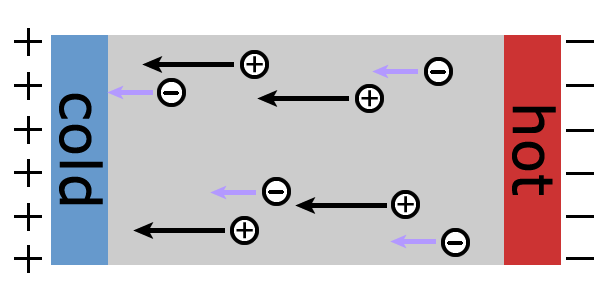
For the most important intrinsic mechanism contributes to the electron transport, the electron-phonon coupling is treated by density functional purterbation theory, and taken into account in the solutions to the Boltzmann transport equation. The variational approach works effeciently for metals (the right image is an illustration to explain the abnormal sign of Seebeck coefficient in lithium based on the calculations) or heavily-doped semiconductors, and the relaxation time approximation can yield useful information of life time and mean free path of electrons. This computational method is implemented in the ABINIT package.

The lattice conductivity can be accurately calculated by the temperature-dependent effective potential method developed by Dr. O. Hellman (TDEP). Therefore, all quantities related to the thermoelectric figure of merit can be evaluated from first-principles calculations, which can provide unbiased predictions, being parallel to the experimental studies.

Phase transitions

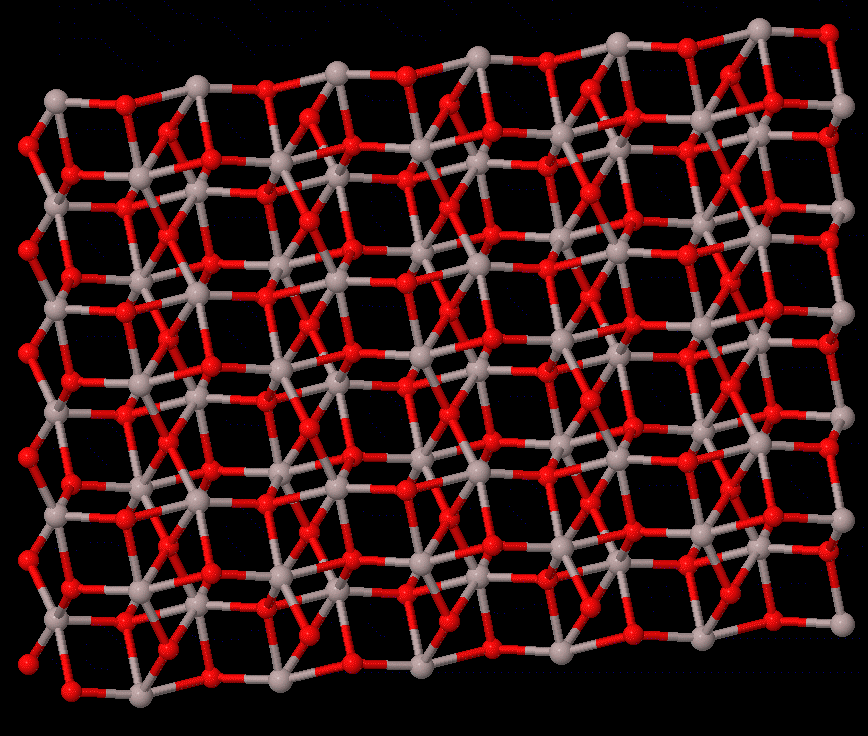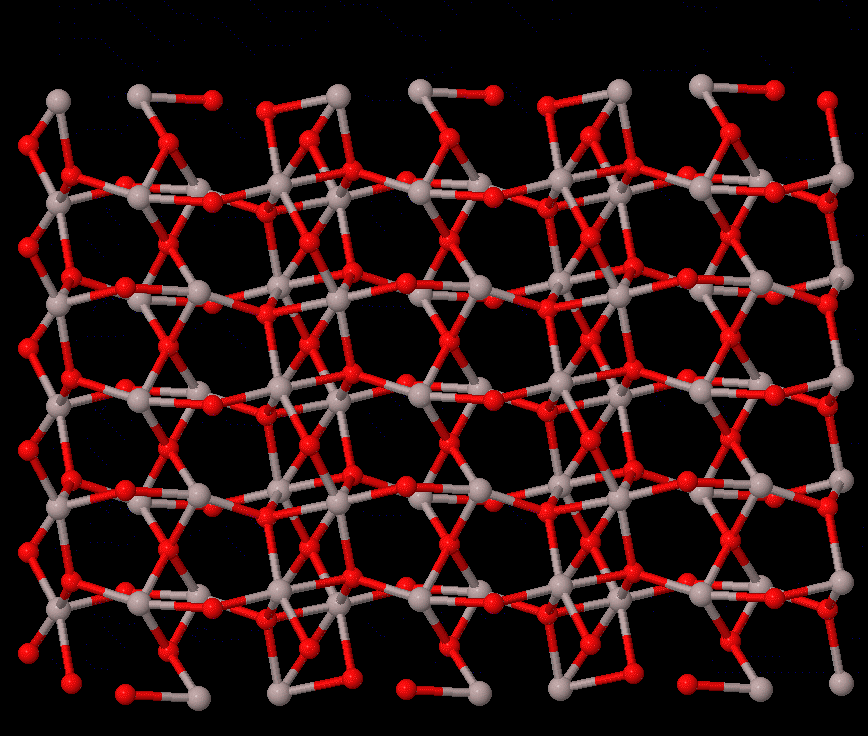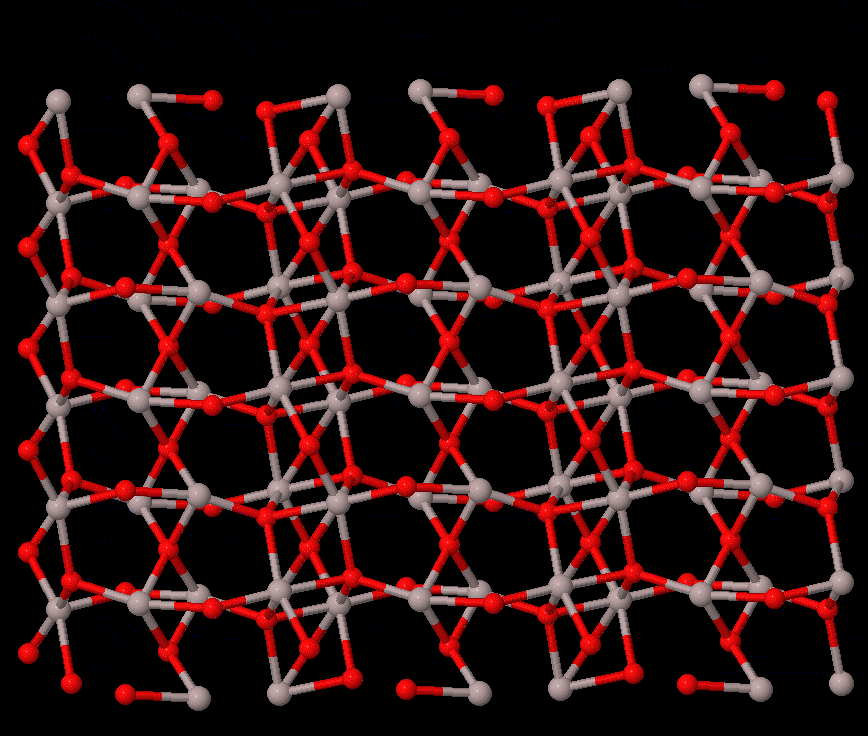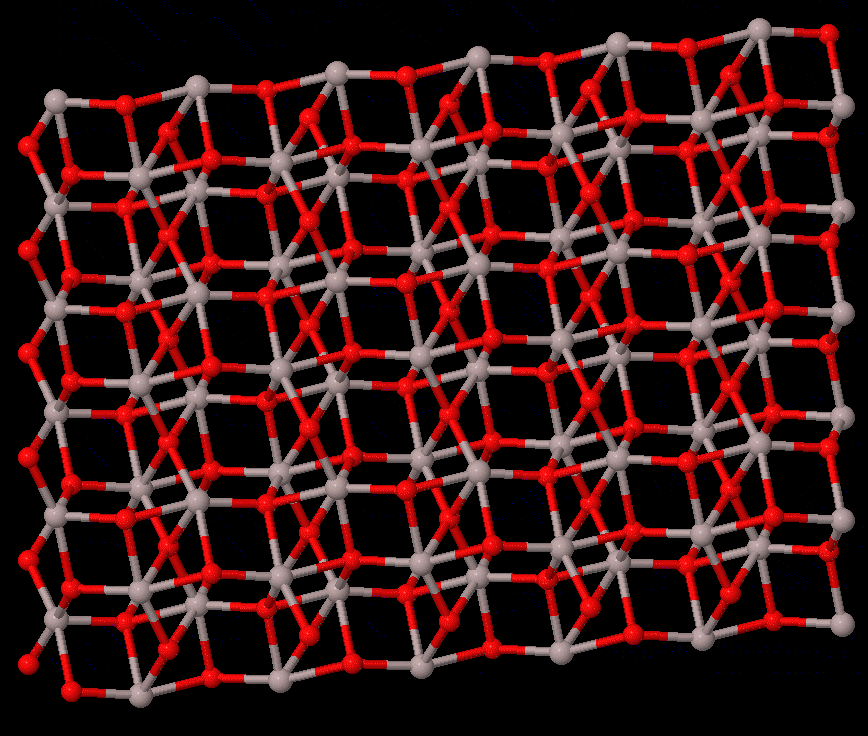
Phase transitions concern the stability of different states of a system, which are fundamental to all studies that rely on the material struture. For solid-solid transtions, lattie vibrations or phonons often play a central role. The reconstructive transition has significant change in the structure, and it is usually of first order. The phonon contribution to the free energy may be the main cause of the transition, which can be calculated by first-principels methods, e.g., quasi-harmonic approximation, or the more accurate temperature-dependent effective potential method. On the other hand, the displacive-type transition is driven by dynamic instability (soft phonon), for which phonon calculations can provide valuable information to calrify the nature of the transition.

The study of transition pathway is also within the scope. For transtions that can be described by group-subgroup or common-subgroup relations (an example of corundum to Rh2O3(II) transition in Al2O3 is illustrated on the right), energetically favarable pathways can be defined, with which the energetic path and kinetic barriers can be computed; therefore, meta-stability of a structure can be understood.